.png)
Wyznaczanie kąta dwóch wektorów, jeœli znane są ich współrzędne.
Niech będą dwa niezerowe wektory $\overrightarrow{u}=[u_{x}, u_{y}]$ oraz $\overrightarrow{v}=[v_{x}, v_{y}]$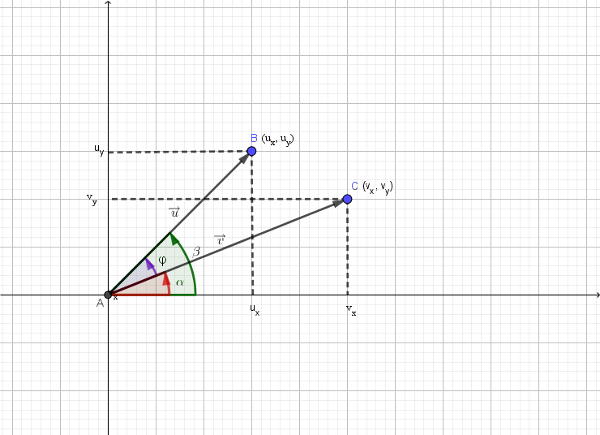
Z definicji kąta kierunkowego odczytujemy z rysunku, że: $$sin(\alpha)= \frac{v_{y}}{v}$$ $$cos(\alpha)= \frac{v_{x}}{v}$$ $$sin(\beta)= \frac{u_{y}}{u}$$ $$cos(\beta)= \frac{u_{x}}{u}$$
gdzie $$v=\sqrt{v_{x}^2+v_{y}^2}, \ u=\sqrt{u_{x}^2+u_{y}^2}$$
Oznaczmy kąt pomiędzy wektorami $\overrightarrow{u}$ oraz $\overrightarrow{v}$ przez $\varphi$
Z rysunku widzimy, że:
$\varphi=\beta – \alpha$
Stąd $$cos(\varphi)=cos(\beta – \alpha)=cos(\alpha)\ cos(\beta)+sin(\alpha)\ sin(\beta)=\frac{v_{x}}{v}\ \frac{u_{x}}{u}+ \frac{v_{y}}{v} \frac{u_{y}}{u}$$ $$sin(\varphi)=sin(\beta – \alpha)=cos(\alpha)\ sin(\beta) – sin(\alpha) \ cos(\beta)=\frac{v_{x}}{v}\ \frac{u_{y}}{u} – \frac{v_{y}}{v}\ \frac{u_{x}}{u}$$
czyli $$cos(\varphi)=\frac{v_{x} u_{x}+v_{y} u_{y}}{vu}$$ $$sin(\varphi)=\frac{v_{x} u_{y}-v_{y}u_{x}}{vu}=\frac{1}{vu}\cdot det\begin{bmatrix} v_{x} & v_{y} \\ u_{x} & u_{y} \\ \end{bmatrix}$$ a
Ze wzorów tych wynikają ważne własności
$$(1)\ vu\cdot cos(\varphi)=v_{x} u_{x}+v_{y} u_{y}$$ $$(2)\ vu\cdot sin(\varphi)= det\begin{bmatrix} v_{x} & v_{y} \\ u_{x} & u_{y} \\ \end{bmatrix}$$
Równośæ (1) naxywamy iloczynem ska;arnym dwóch niezerowych wektorów i oznaczamy $$ \overrightarrow{v} \circ \overrightarrow{u} = uv \cdot cos(\varphi)$$ gdzie
$$ \overrightarrow{v} \circ \overrightarrow{u} = v_{x} u_{x}+ v_{y} u_{y}$$
Równośæ (2) nazywamy wyznacznikiem dwóch wektorów, którego wartośæ bezwzlędna jest równa polu równoległoboku wyznaczonego przez wektory $\overrightarrow{v}$ oraz $ \overrightarrow{u}.$
$$\|vu\cdot sin(\varphi)\|= \| det\begin{bmatrix}
v_{x} & v_{y} \\
u_{x} & u_{y} \\
\end{bmatrix}\|$$
Pole trójkąta wyznaczonego przez wektory $\overrightarrow{v}$ oraz $ \overrightarrow{u}.$ jest równe połowie pola równoległoboku. $$P_{tr}= \frac{1}{2}\cdot \| det \begin{bmatrix} v_{x} & v_{y} \\ u_{x} & u_{y} \\ \end{bmatrix}\|$$
PrzykładPole trójkąta wyznaczonego przez wektory $\overrightarrow{v}$ oraz $ \overrightarrow{u}.$ jest równe połowie pola równoległoboku. $$P_{tr}= \frac{1}{2}\cdot \| det \begin{bmatrix} v_{x} & v_{y} \\ u_{x} & u_{y} \\ \end{bmatrix}\|$$
Oblicz pole trójkąta pokazanego na rysunku poniżej
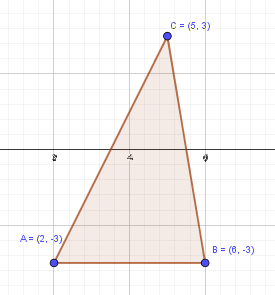$$\overrightarrow{AC}=[5-2,3+3]=[3, 6]$$
$$\overrightarrow{AB}=[6-2, -3+3]=[4, 0]$$
$$P_{trABC}= \frac{1}{2}\cdot \|det \begin{bmatrix}
3 & 6 \\
4 & 0 \\
\end{bmatrix}\|=\frac{1}{2}\cdot \|0-24\|=\frac{1}{2}\cdot \|-24\|=12$$Odp.
Pole trójkąta wynosi $12j^{2}$.
Zadanie
Napisz program obliczający pole dowolnej figury wypukłej. W programie podajemy wierzchołki figury w postaci par liczb.
